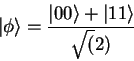


Next: Application: Superdense coding
Up: A Quantum Computing Tutor
Previous: A Quantum Computing Tutor
Contents
Modern classical computers store and manipulate a unit of information called
the bit, which takes either 0 or 1 as it's value. The classical paradigm
seems to be limited however in the types of problems it can solve; there is a
vast amount of problems that are intractable on modern computers. Herein lies
the promise of Quantum Computers. A Quantum Computer uses a different
fundamental unit of information, called the Qubit. A Qubit
has two base states, normally denoted by the Dirac notation,
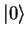 and
and 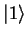 . The difference between a qubit and a classical bit, is
that it is possible for a qubit to be in a linear combination of states, denoted by;
. The difference between a qubit and a classical bit, is
that it is possible for a qubit to be in a linear combination of states, denoted by;
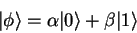 |
(3) |
The numbers 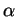 and
and 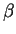 are complex numbers. The property of being able
to exist in multiple states is called superposition. Quantum mechanics
does not allow us to view what the amplitudes, ie.
are complex numbers. The property of being able
to exist in multiple states is called superposition. Quantum mechanics
does not allow us to view what the amplitudes, ie. 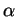 and
and 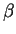 , of the
two basevectors are. Instead, when we measure a qubit, we get the state
, of the
two basevectors are. Instead, when we measure a qubit, we get the state
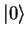 with probability
with probability 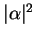 , and the state
, and the state 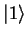 with
probability
with
probability 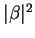 . Both of these probabilities must add up to 1. If a
quantum operation is performed on a qubit in multiple states, then the
operation is performed on all states simultaneously. When the qubit is
observed, it will collapse back into a single state stochastically, according
to the squares of the probabilities.
. Both of these probabilities must add up to 1. If a
quantum operation is performed on a qubit in multiple states, then the
operation is performed on all states simultaneously. When the qubit is
observed, it will collapse back into a single state stochastically, according
to the squares of the probabilities.
The famous physicist R. Feynmann suggested that a qubit
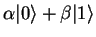 occupies all the states between 0 and 1
simultaneously, but collapses into 0 or 1 when observed physically.
A qubit can therefore encode an infinite amount of information, but most of
this information is useless as it can never be observed. This raises all kinds
of interesting philosophical questions about what information is. As stated
previously, when observed, a qubit collapses into one of it's basis states. No
one knows why this happens, it is one of the basic tenets of quantum mechanics.
The explanation that a quantum state collapses upon physical observation is
known as the Copenhagen Interpretation, and is the standard(though
not the only) way of explaining the collapse upon measurement.
occupies all the states between 0 and 1
simultaneously, but collapses into 0 or 1 when observed physically.
A qubit can therefore encode an infinite amount of information, but most of
this information is useless as it can never be observed. This raises all kinds
of interesting philosophical questions about what information is. As stated
previously, when observed, a qubit collapses into one of it's basis states. No
one knows why this happens, it is one of the basic tenets of quantum mechanics.
The explanation that a quantum state collapses upon physical observation is
known as the Copenhagen Interpretation, and is the standard(though
not the only) way of explaining the collapse upon measurement.
Superposition is one of the properties that allows the Quantum Computing
paradigm to supercede classical computing. The other is entanglement.
A two qubit system has four computational basis states, which are 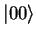 ,
,
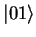 ,
, 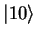 and
and 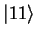 . The two qubit system can be in any
superposition of these states. There are four very interesting states that
such a system can be prepared in. These states are refered to as the Bell
States or EPR states. An example of one of these states is the following;
. The two qubit system can be in any
superposition of these states. There are four very interesting states that
such a system can be prepared in. These states are refered to as the Bell
States or EPR states. An example of one of these states is the following;
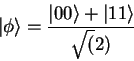 |
(4) |
When one measures the first qubit in this state, there are two possible
results; 0 with probability 1/2 leaving the other qubit in the state
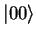 , and 1 with probability 1/2, leaving the other qubit in the state
, and 1 with probability 1/2, leaving the other qubit in the state
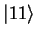 . This means that when the second qubit is measured it will
always be in the same state as the first qubit! This correlation between
the qubits is known as entanglement. Bell proved that the measurement
correlations between the two qubits are stronger than could ever exist
between classical systems. For example, entanglement between two qubits
can persist even thought they are spatially seperated. Bell states are
used as the basis of quantum teleportation and super-dense coding.
. This means that when the second qubit is measured it will
always be in the same state as the first qubit! This correlation between
the qubits is known as entanglement. Bell proved that the measurement
correlations between the two qubits are stronger than could ever exist
between classical systems. For example, entanglement between two qubits
can persist even thought they are spatially seperated. Bell states are
used as the basis of quantum teleportation and super-dense coding.
The properties of entanglement and superposition mean that certain speedups
can be used in quantum algorithms that will never be achievable on classical
computers. The two most famous quantum algorithms are Shor's algorithm, which
can factor a number which is the product of two large primes in exponential
time, and Grover's algorithm which searches an unsorted database in
quadratic time.



Next: Application: Superdense coding
Up: A Quantum Computing Tutor
Previous: A Quantum Computing Tutor
Contents
Colm O hEigeartaigh
2003-05-30
![]() and
and ![]() . The difference between a qubit and a classical bit, is
that it is possible for a qubit to be in a linear combination of states, denoted by;
. The difference between a qubit and a classical bit, is
that it is possible for a qubit to be in a linear combination of states, denoted by;