


Next: libplot
Up: The Bloch Sphere
Previous: Background Quantum Mechanics
Contents
The numbers 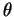 and
and 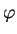 in equation (2) define a point on the unit three-dimensional
sphere. This sphere is called the Bloch Sphere. It provides a useful means of
visualizing the state of a single qubit. However, there is no simple
generalization of the Bloch sphere known for multiple qubits.
in equation (2) define a point on the unit three-dimensional
sphere. This sphere is called the Bloch Sphere. It provides a useful means of
visualizing the state of a single qubit. However, there is no simple
generalization of the Bloch sphere known for multiple qubits.
The north pole of the sphere is assigned the state 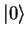 and the south pole the state
and the south pole the state 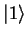 .
A classical bit would be represented on the bloch sphere as being either at the north pole of the
sphere or at the south pole. A qubit however, can be a point anywhere on the surface of the sphere.
The bloch sphere is not a precise indicator of where the qubit lies on the unit sphere,
it merely shows the latitude of the qubit. The latitude defines how close the qubit is to the poles,
depending on the probability amplitudes.
.
A classical bit would be represented on the bloch sphere as being either at the north pole of the
sphere or at the south pole. A qubit however, can be a point anywhere on the surface of the sphere.
The bloch sphere is not a precise indicator of where the qubit lies on the unit sphere,
it merely shows the latitude of the qubit. The latitude defines how close the qubit is to the poles,
depending on the probability amplitudes.
The sphere has 3 axes; x, y and z. The number 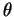 defined in equation (2) gives the angle of
the qubit from the vertical z axis. This angle is easily found in the following way: we have already
seen that equation (1) can be written as equation (2). By comparing the
defined in equation (2) gives the angle of
the qubit from the vertical z axis. This angle is easily found in the following way: we have already
seen that equation (1) can be written as equation (2). By comparing the 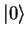 parts of both
equations we get;
parts of both
equations we get;
Since 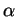 is known,
is known, 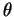 can be found by;
can be found by;
It is impossible to solve the equation to find out where the qubit exists on the semicircle defined
by the longitude. The qubit exists on every point on that semicircle, so in the bloch sphere
implementation for the Quantum Computing Language, the qubit is assigned an arbitrary longitude of 70
pixels from the vertical z axis.



Next: libplot
Up: The Bloch Sphere
Previous: Background Quantum Mechanics
Contents
Colm O hEigeartaigh
2003-05-30
![]() and
and ![]() in equation (2) define a point on the unit three-dimensional
sphere. This sphere is called the Bloch Sphere. It provides a useful means of
visualizing the state of a single qubit. However, there is no simple
generalization of the Bloch sphere known for multiple qubits.
in equation (2) define a point on the unit three-dimensional
sphere. This sphere is called the Bloch Sphere. It provides a useful means of
visualizing the state of a single qubit. However, there is no simple
generalization of the Bloch sphere known for multiple qubits.